STAT 804: Lecture 18 Notes

Forecast standard errors

You should remind yourself that the computations of conditional expectations we have made used the fact that the a's and b's are constants - the true parameter values. In fact we then replace the parameter values with estimates. The quality of our forecasts will be summarized by the forecast standard error:

We will compute this ignoring the estimation of the parameters and then discuss how much that might have cost us.

If then so that our forecast standard error is just the variance of .

Consider first the case of an AR(1) and one step ahead forecasting:

The variance of this forecast is so that the forecast standard error is just .

For forecasts further ahead in time we have

and

Subtracting we see that

so that we may calculate forecast standard errors recursively. As we can check that the forecast variance converges to

which is simply the variance of individual Xs. When you forecast a stationary series far into the future the forecast error is just the standard deviation of the series.

Turn now to a general ARMA(p,q). Rewrite the process as the infinite order AR

to see that again, ignoring the truncation of the infinite sum in the forecast we have

so that the one step ahead forecast standard error is again .

Parallel to the AR(1) argument we see that

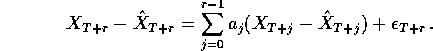
The errors on the right hand side are not independent of one another so that computation of the variance requires either computation of the covariances or recognition of the fact that the right hand side is a linear combination of .

A simpler approach is to write the process as an infinite order MA:

for suitable coefficients . Now if we treat conditioning on the data as being effectively equivalent to conditioning on all for t ;SPMlt; T we are effectively conditioning on for all t;SPMlt;T. This means that

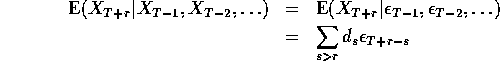
and the forecast error is just

so that the forecast standard error is

Again as this converges to .

Finally consider forecasting the ARIMA(p,d,q) process where W is ARMA(p,q). The forecast errors in X can clearly be written as a linear combination of forecast errors for W permitting the forecast error in X to be written as a linear combination of the underlying errors . As an example consider first the ARIMA(0,1,0) process . The forecast of is just 0 and so the forcast of is just

The forecast error is

whose standard deviation is . Notice that the forecast standard error grows to infinity as . For a general ARIMA(p,1,q) we have

and

which can be combined with the expression above for the forecast error for an ARMA(p,q) to compute standard errors.

Software

The S-Plus function arima.forecast can do the forecasting.

Comments

I have ignored the effects of parameter estimation throughout. In ordinary least squares when we predict the Y corresponding to a new x we get a forecast standard error of

which is

The procedure used here corresponds to ignoring the term which is the variance of the fitted value. Typically this value is rather smaller than the 1 to which it is added. In a 1 sample problem for instance it is simply 1/n. Generally the major component of forecast error is the standard error of the noise and the effect of parameter estimation is unimportant.

In regression we sometimes compute perdiction intervals

The multiplier c is adjusted to make the coverage probability close to a desired coverage probability such as 0.95. If the errors are normal then we can get c by taking . When the errors are not normal, however, the error in is dominated by which is not normal so that the coverage probability can be radically different from the nominal. Moreover, there is no particular theoretical justification for the use of t critical points. However, even for non-normal errors the prediction standard error is a useful summary of the accuracy of a prediction.